What is the smallest signal we can measure with the ActiveTwo bitstep of 31 nVolt ?
 
During the past years, we have been surprised by the different views that live among researchers about what exactly is going on during the sampling and averaging process. The answers we hear on the resolution problem, can generally be divided into three groups.
 
Before reading on, choose which answer you would support :
 
a) The smallest measurable signal is determined by the amplifier noise level, you cannot measure signals which are drowned in amplifier noise. This is exactly why it is so important to buy the system with the lowest amplifier noise.
b) The smallest measurable signal is determined by the Least Significant Bit (LSB) value of the analog-to-digital converter (ADC). Signal changes smaller than the LSB value will not be able to force the ADC to the next digital level. Adding averaging does not make a principle difference: signals smaller than the LSB value are ignored in every single triggered sweep, so they can never be recovered from the data by taking an average of all these sweeps. Therefore we want a system with maximum gain to get the smallest possible LSB.
c) There isn't any principle lower limit for the smallest measurable signal, the resolution is entirely determined by practical limits, such as the maximal amount of trials that can be done in an ERP experiment.
 
 
If you have answered c, you have a very good understanding of the matter, so no need to read further, do not waste time reading this FAQ, continue with your experiments, you are doing a good job !
 
If you have chosen a), you do not fully understand what averaging of triggered sweeps can do to improve the Signal to Noise ratio (SNR). The nice thing about signals evoked by a stimulus is that they allow you to repeat an experiment many times. The evoked signal will be synchronized with the trigger in every sweep, whereas the total noise is random in the sweeps: the noise wave form is different in every sweep, and not correlated with the trigger moments. Summation of sweeps will increase the amplitude of the evoked response proportional with the number of sweeps. The total noise is not synchronized with the triggers, and therefore the power (not the amplitude) of the noise will increase proportional with the number of sweeps . Because amplitude is the square root of power, the ratio between signal amplitude and noise amplitude will increase with the square root of the number of sweeps. This makes it possible to recover small signals which were drowned in noise, provided of course that you can setup an experiment to take enough sweeps. Two things are important to realize:
     
  1) The total noise level is a sum of several uncorrelated noise sources:
amplifier noise, electrode noise, mains interference, but also physiological signals like background EEG, EMG and ECG. The power of uncorrelated noise sources add. For the noise amplitude this means that:
   
 
    The quadratic addition means that only the larger noise sources determine the total noise, smaller noise sources have hardly any effect on the total noise. In a practical ERP experiment, this means that background EEG (10-100 uVpp) fully determines the noise level, electrode noise (5-10 uVpp) and amplifier noise (3-5 uV) add only a few percent to the total noise level.
     
  2) Because the signal-to-noise ratio (SNR) only increases with the square root of the number of sweeps, a lot of sweeps will be needed to extract small signals. For example: extracting a 100 nV signal from 100 uV background EEG will take a at least a million sweeps. So, increasing the SNR in the separate sweeps by appropriate filtering remains important.
 

Answer b) sounds very logical, but it is to pessimistic because it does not appreciate what dithering can do to improve the resolution of an ADC.

The reasoning followed in answer b) is valid when the LSB value is larger than the total peak-to-peak noise level (background EEG + electrode + amplifier noise). In this case, the ADC indeed is only able to capture signals larger than the LSB value. However, when one or more LSBs are smaller than the noise, these LSB are constantly toggling between values due to the noise input -in technical terms:these bits are dithered- and the capturing of small signals becomes a purely statistical effect. It is amazing to see that even the technical departments of some well know manufacturers do not seem to understand this and they keep speaking of LSB values in terms of "minimum resolvable signal" Consider for example a system with 1 uV LSB value. Now suppose that a small 0.1 uV ERP signal is riding on a 10 uVpp total noise floor. In 9 out of 10 sweeps, the large 10uVpp total noise signal fully determines the ADC output and the 0.1 uV signal won't be able to drive the ADC to its next level. However, in 1 out of 10 sweeps there will occur the situation where the 0.1uV signal is enough to change the LSB of the ADC. After averaging a large number of sweeps, a perfect 0.1 uV signal will appear on screen, even though the original sweeps are captured with an 1 uV resolution. The 1 uV LSB value is used in our previous 16 bit ActiveOne system, and our customers have indeed been able to measure very clean small ERP signals with the system, see this ERP example. The extra 5 LSBs in the ActiveTwo (LSB is 31.25 nV) makes the averaging process a little more precise, resulting in minor improvements of SNR of the averages, but there is not an essential difference with the 1 uV example given above.
 
So, signals buried in noise are quantized in all the LSBs below the noise level. However, it is important to realize that most of the information is already captured by the "most significant noise bit" (the first bit below the amplifier noise level). Even more important is that the LSB value does not impose any limit on the smallest detail in the signal that can be recovered with averaging. In other words: the ActiveTwo system is well capable of recovering signal details smaller than 31.25 nV.

Some competing system with adjustable gain are able to select even smaller LSB values than we use in our new ActiveTwo system. Customers often ask us how much effect adding more LSBs buried in noise actually has. As an example, we can calculate the difference in performance between ActiveTwo's 31.25 nV LSB (with DC amplifier and 524 mVpp input range), and the 7 nV LSB of typical competing AC design on it's highest gain setting on it's highest gain setting (with DC measurements eliminated, and a mere 400 uV input range).

The input noise caused by the analog amplifier circuitry of both the competing sytem and the ActiveTwo system is approx. 0.5 uVrms for a 100 Hz bandwidth (approx. 2 uVpp, all contemporary systems are near this value). The digitalization process generates quantization noise, this is extra noise caused by the introduced "steps" in the signal (the smooth signal becomes like a staircase, the steps represent extra noise). The amount of quantization noise is proportional with the LSB value (large steps add much noise): noise theory predicts that the quantization noise has a magnitude of LSB/Ö12 (approx. 0.3 LSB). So, the ActiveTwo adds 31.25/Ö12 = 9 nVrms quantization noise, whereas the competing system adds 7/Ö12 = 2 nVrms. The amplifier noise and quantization noise are independent noise sources, so the powers of these noise sources should be added to find the total noise level. See formula given above. Lets see how this works out when we do this calculation for both the ActiveTwo, and for the competing system on its highest gain setting:

Competitor: total noise = Ö{ (amp noise)^2 + (quan noise)^2 } = Ö{ (0.5)^2 + (0.002)^2 } = 0.500004 uVrms
ActiveTwo: total noise = Ö{ (amp noise)^2 + (quan noise)^2 } = Ö{ (0.5)^2 + (0.009)^2 } = 0.50008 uVrms

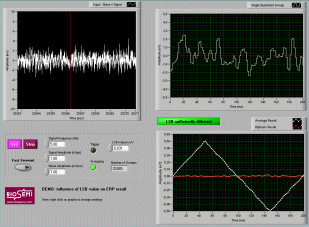
In a real-world ERP measurement, this difference in noise would even be smaller than this 0.02% because the noise level is not determined by the relatively small 2 uVpp amplifier noise, but by the 10-100 uV of background EEG. The effect described above can be visualized with a simple LabVIEW demonstration program which can be downloaded from here. You need the LabVIEW Run Time Engine to be able to run this program. When you experiment with various settings for noise amplitude, signal amplitude and LSB, the program will be very educational showing the averaging of ERPs which are drowned in noise. The demonstration shows 5 effects:
     
Click on the picture to download demonstration program    
1) The averaging process only works properly so long as one or more LSBs are dithered by noise. For a given LSB value, decreasing the noise will actually lead to a too low noise level, resulting in corruption of the average results.
2) If the LSB is not dithered, meaningful average results can only be calculated for signals much larger than the LSB.
3) Provided the LSB is dithered, signals smaller than the LSB can be averaged out of the noise without any problem. The LSB is no "magic border" whatsoever, there is a gradually decrease of SNR when the signal amplitude is decreased below the LSB value.
4) Provided the LSB is dithered, SNR of the average increases with the square root of the number of sweeps. Because of the square root relation, the first few sweeps make the most difference, after many sweeps, it takes a lot of time to see improvements. Recovering a small signal from a lot of noise is always possible, but it might take a lot of sweeps (and time).
5) Decreasing the LSB below approx. 1/10th of the peak-to-peak noise, has no significant effect on the SNR of the average result.
   
 
So, the strange thing about noise is that you do not want too much of it (because the averaging process would take too long), but that you also do not want too less of it (because the LSB has to be dithered).
 
The demonstration program allows you to simulate the LSB values and average results of several systems from BioSemi and it's competitors. All commercially available systems have an input noise in the order of 3uVpp (100 Hz bandwidth) and have their LSB small enough to be sufficiently dithered. Consequently you won't see much difference between the systems in terms of ERP result. Your choice between the systems therefore has to be based on other features.